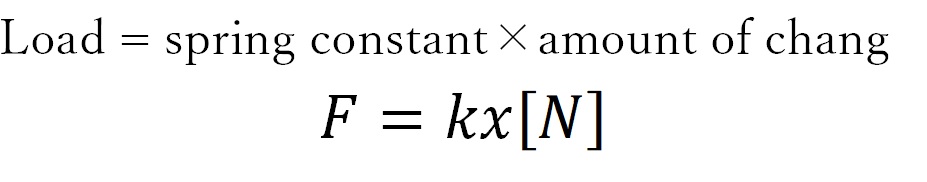| |
If you're involved in anything about springs, you'll definitely hear the word "Hooke's law."
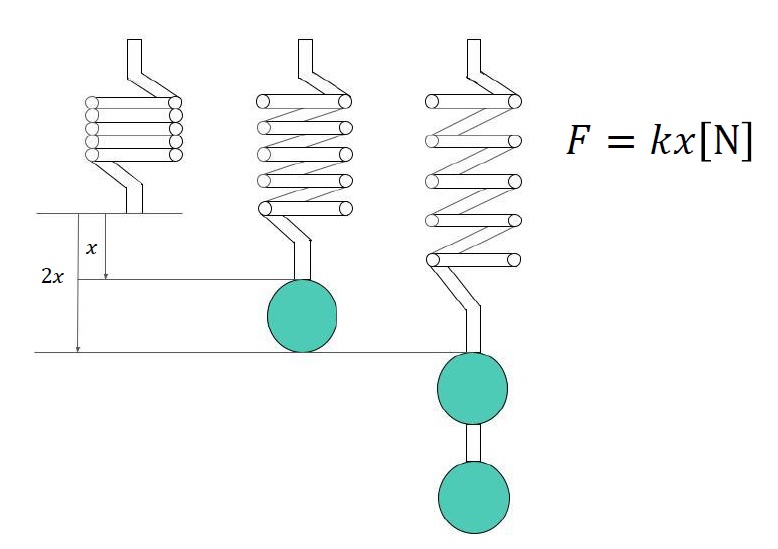
Hooke's law is "the law that the elongation of a spring is proportional to the pulling force" . As shown in the above figure, we will conduct an experiment to hang a weight on a spring. At that time, if the size of the weight is doubled, the elongation of the spring will be doubled, and even if the weight is further increased, the elongation of the spring will change proportionally.
The formula is as follows.
The magnitude (load) of the force applied to the spring is F [N]
The length of expansion and contraction (deformation amount) of the spring is χ [m]
The relationship is as follows:
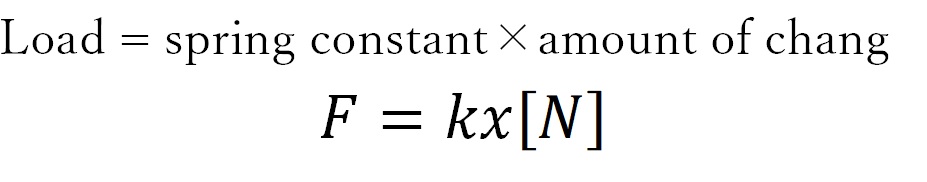
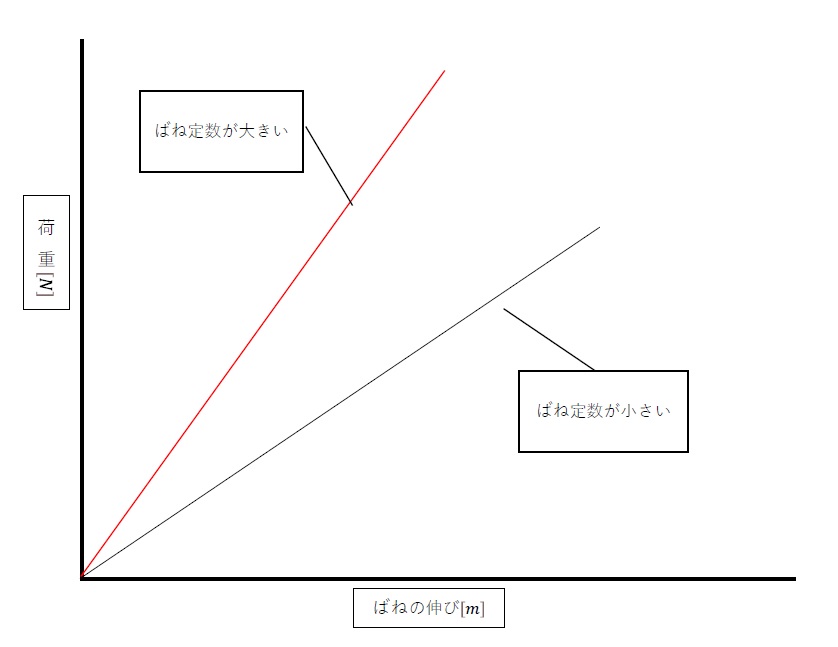
In addition, k is a proportional constant called the spring constant, which indicates the slope of the graph when this relationship is expressed as shown in Fig. 1. Therefore, the larger the spring constant k, the larger the force required to extend the spring.
Fig. 1
Click here for more information ↓
> Spring dynamics terminology (1) What is spring constant?(Japanese page)
About Robert Hooke
This law was discovered by Robert Hooke, a 17th century British scientist (at that time a naturalist). It is a person named 1635-1703).
In 1678, Hook gave a "Lecture on Restoring Force" in a public lecture called Cutler Lecture, in which he discussed "Hooke's Law" that spring elongation is proportional to force.
The hook was a simple experiment of expansion and contraction of the spring, and the invisible force could be seen as the expansion and contraction of the spring.
* At that time, the concepts of "force," "pressure," and "energy" had not yet been established.
In addition to "Hooke's Law", Hook's research field is very wide, and he is also the person who published detailed sketches using a microscope as "Micrographia". Furthermore, when observing the cork used in wine etc., he named it "cell", which means a cell in a structure like a small room.
He also worked as an assistant to Robert Boyle, known for "Boyle's Law," in which the volume of gas under constant temperature is inversely proportional to pressure.

|
|

![]()